All Python code for back testing these algorithmic trading strategies can be found at the following GitHub Repo: https://github.com/hermessuen/algoTrading

Cross- Sectional Mean Reversion in Python: Cross sectional mean reversion represents the hypothesis that within a specific universe of stocks, say the S&P 500, the daily returns of all of the stocks will revert to the mean of the daily returns of all the stocks in that universe. A weighting is assigned to each stock, dependent on how far away its most recent close is away from the mean of the daily return of all the stocks. The weights sum up to "1".

Use this weight allocation to determine how your capital should be allocated This is a daily re-balancing strategy. Some parameters one could tune are the time period to which the mean is calculated, the universe of stocks, and the weighting scheme. A simple normalization scheme was used here. The stock universe are the bottom 200 stocks in the S&P500. This example was adopted and tweaked from Ernie Chan's book

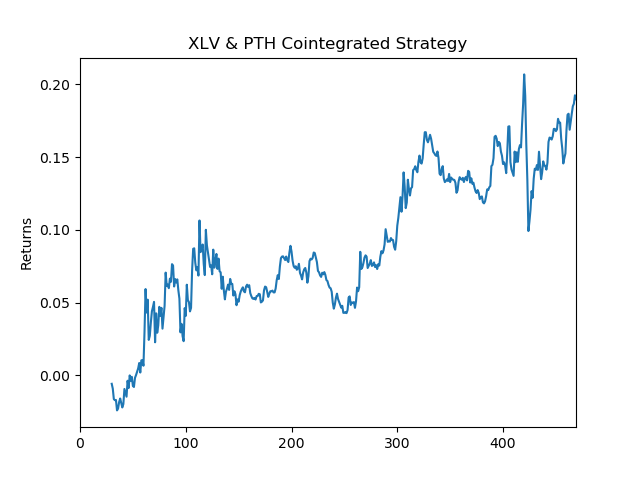
Co-Integration Mean- Reversion in Python: This refers to the hypothesis that although single ETFs may not be mean-reverting, a combination of them may be mean-reverting. The python script to develop a strategy for co-integrating the healthcare ETFs "XLV" and "PTH" involves a series of tests. First, a series of well-known statistical tests are performed in an effort to reject the hypothesis that a combination of the two ETFs are NOT mean-reverting. By mean reverting we mean that the the next time step in the price series of the two ETFs is dependent on the mean of the previous time steps. Even if we cannot reject this hypothesis with more than 90% certainty, we can still use the result of the statsitical test for to determine a "lookback" period. A look-back period is calculated in this script based on the first statistical test. This lookback period is used to determine the hedge ratio between the two ETFs. A dynamically changing hedge ratio is then calculated. The script then tests a linear strategy that simply invests more into the combination of the two ETFs if they are further away from their previous lookback mean. To measure the performance of the strategy, the Sharpe Ratio, daily returns, and APR are calculated.